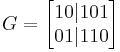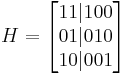Parity-check matrix

In coding theory, a parity-check matrix of a linear block code C is a generator matrix of the dual code. As such, a codeword c is in C if and only if the matrix-vector product Hc=0.

The rows of a parity check matrix are parity checks on the codewords of a code. That is, they show how linear combinations of certain digits of each codeword equal zero. For example, the parity check matrix

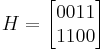
H = \begin{bmatrix} 0011\\ 1100 \end{bmatrix}

specifies that for each codeword, digits 1 and 2 should sum to zero (according to the second row) and digits 3 and 4 should sum to zero (according to the first row).

Creating a parity check matrix

The parity check matrix for a given code can be derived from its generator matrix (and vice-versa). If the generator matrix for an [n,k]-code is in standard form

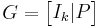G = \begin{bmatrix} I_k | P \end{bmatrix},

then the parity check matrix is given by

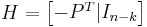H = \begin{bmatrix} -P^T | I_{n-k} \end{bmatrix},

because

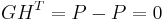G H^T = P-P = 0.

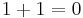Negation is performed in the finite field mod q. Note that if the characteristic of the underlying field is 2 (i.e., 1%2B1=0 in that field), as in binary codes, then 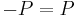-P=P, so the negation is unnecessary.

For example, if a binary code has the generator matrix

G = \begin{bmatrix} 10|101 \\ 01|110 \\ \end{bmatrix}

The parity check matrix becomes

H = \begin{bmatrix} 11|100 \\ 01|010 \\ 10|001 \\ \end{bmatrix}

For any valid codeword 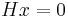x, Hx = 0. For any invalid codeword 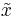\tilde{x}, the syndrome S satisfies 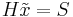H\tilde{x} = S.

See also

References